Тип Д29 C2 № 19778 
Механика (расчетная задача). Динамика
i
Решение.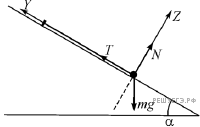 
1. Малые колебания в системе без трения будут гармоническими, если возвращающая сила пропорциональна смещению грузика от положения равновесия. Решение задачи можно провести двумя способами: динамическим, исходя из второго закона Ньютона, и энергетическим, используя закон сохранения механической энергии. Будем использовать динамический подход.
2. Введем систему координат, у которой ось Z направлена перпендикулярно наклонной плоскости, ось Y — вверх, вдоль нити в положении равновесия, а ось X — перпендикулярно нити вдоль плоскости. Нарисуем силы, действующие на грузик (силу тяжести mg, силу нормальной реакции N и силу натяжения нити T), и изобразим вид системы сбоку, вдоль плоскости (см. рис.).
3. Вдоль оси Z грузик не движется, поэтому 
Вдоль оси Y грузик при малых колебаниях, то есть при малых смещениях вдоль оси X, практически не движется, а сила натяжения отклоняется от оси Y на малые углы 
≈ 
поэтому 
≈ T ≈ 
4. Из второго закона Ньютона в проекции на ось X получаем:
≈ 
≈ 
или 
что является уравнением гармонических колебаний с частотой 
и периодом колебаний
≈ 
≈ 1,6699 ≈ 1,67 с.
Ответ: 
Спрятать критерииКритерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом: (в данном случае: закон сохранения проекции импульса системы тел, закон изменения механической энергии, закон Амонтона-Кулона); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчеты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины. | 3 |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеется один или несколько из следующих недостатков. Записи, соответствующие пунктам II и III, представлены не в полном объеме или отсутствуют. И ( ИЛИ ) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачеркнуты. И ( ИЛИ ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И ( ИЛИ ) Отсутствует пункт V, или в нем допущена ошибка. | 2 |
| Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. | 1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла. | 0 |
| Максимальный балл | 3 |
Ответ: 
= 45° к горизонту, лежит маленький грузик, привязанный невесомой нерастяжимой нитью длиной l = 50 см к вбитому в плоскость гвоздику (см. рис.). Найдите период малых (угол