Тип Д29 C2 № 2950 

Механика (расчетная задача). Кинематика
i
Тело, свободно падающее с некоторой высоты, первый участок пути проходит за время  а такой же последний — за время
а такой же последний — за время  Найдите полное время падения тела t, если его начальная скорость равна нулю.
Найдите полное время падения тела t, если его начальная скорость равна нулю.
Решение. Нарисуем схематично рисунок (в принципе, он не обязателен)
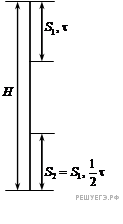
Если t — полное время падения с высоты H, то


Ответ: 
Примечание: поскольку общее время получилось меньше, чем сумма времен на участках  и
и  (
( ), заключаем, что эти участки «перекрывались». Таким образом, рисунок, в большей степени соответствующий реальности, должен выглядеть следующим образом:
), заключаем, что эти участки «перекрывались». Таким образом, рисунок, в большей степени соответствующий реальности, должен выглядеть следующим образом:
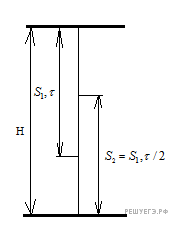
Однако, как и отмечается в самом начале, конкретный вид рисунка не имеет никакого значения, он только помогает написать правильное уравнение.
Спрятать критерииКритерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: формулы кинематики равноускоренного движения); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, и обозначений величин, используемых в условии задачи); III) проведены необходимые математические преобразования, приводящие к правильному ответу; IV) представлен правильный ответ | 3 |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются следующие недостатки. Записи, соответствующие пункту II, представлены не в полном объеме или отсутствуют. ИЛИ В решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачеркнуты; не заключены в скобки, рамку и т. п.). ИЛИ В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца. ИЛИ Отсутствует пункт IV, или в нем допущена ошибка | 2 |
| Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи | 1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла | 0 |
| Максимальный балл | 3 |
Ответ: 
а такой же последний — за время
Найдите полное время падения тела t, если его начальная скорость равна нулю.
и
(
), заключаем, что эти участки «перекрывались». Таким образом, рисунок, в большей степени соответствующий реальности, должен выглядеть следующим образом:




Как такое возможно?! Пусть, время полёта=1.25с. Следовательно, S=gt^2/2=7,8125. Что меньше 10-ти. А из условия известно, что 1 участок пути=2 участку пути=10 м.(потому что тело свободно падает) Поэтому, из условия мы знаем, что S>10, что не соответствует ответу.
Участки накладываются друг на друга. Их общий путь меньше суммы.
Почему H-S2=H-S1?
Потому что
Эту задачу можно решить ещё одним способом.
1.находим скорость тела в конце первого участка Vk1=g*t=10*1=10 м/с.
2. Находим начальную скорость при входе в последний участок
S=V02*t + g*t*t/2
5=V02*(1/2) + (10/2)*(1/2)*(1/2)
10=V02 + (5/4) => V02=8,75 m/c
Сравниваем скорости Vk1>V02 => 10>8,75.
Значит участки перекрываются (см. чертёж).
Значит надо из суммарного времени полёта по условию задачи вычесть двойное время пролёта участка перекрытия. Это время легко найти зная скорость V02 и Vk1
Vk1=V02+g*t => 10=8,75 +10*t => t=0,125 сек
Окончательно получаем время Полёта:
tполёта= 1c + 0,5c - 2*0,125= 1,25 c.