Тип Д29 C2 № 3813 
Раздел кодификатора ФИПИ/Решу ЕГЭ: Механика (расчетная задача). Движение по окружности
i
Система из грузов m и M и связывающей их легкой нерастяжимой нити в начальный момент покоится в вертикальной плоскости, проходящей через центр закрепленной сферы. Груз m находится в точке А на вершине сферы (см. рис.). В ходе возникшего движения груз m отрывается от поверхности сферы, пройдя по ней дугу 30°. Найдите массу m, если М = 100 г. Размеры груза m ничтожно малы по сравнению с радиусом сферы. Трением пренебречь. Сделайте схематический рисунок с указанием сил, действующих на грузы.
Решение.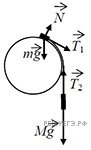 
1. Будем считать систему отсчета, связанную с Землей, инерциальной.
2. На рисунке показан момент, когда груз
еще скользит по сфере. Из числа сил, действующих на грузы, силы тяжести 
и 
потенциальны, а силы натяжения нити 
и 
а также сила реакции опоры 
непотенциальны. Поскольку нить легкая и трения нет, 
Сила направлена по скорости 
груза m, а сила 
— противоположно скорости 
груза 
Модули скоростей грузов в один и тот же момент времени одинаковы, поскольку нить нерастяжима. По этим причинам суммарная работа сил и при переходе в данное состояние из начального равна нулю. Работа силы также равна нулю, так как из-за отсутствия трения 
3. Таким образом, сумма работ всех непотенциальных сил, действующих на грузы m и M, равна нулю. Поэтому в инерциальной системе отсчета, связанной с Землей, механическая энергия системы этих грузов сохраняется.
4. Найдем модуль скорости груза m в точке его отрыва от поверхности сферы. Для этого приравняем друг другу значения механической энергии системы грузов в начальном состоянии и в состоянии, когда груз m находится в точке отрыва (потенциальную энергию грузов в поле тяжести отсчитываем от уровня центра сферы, в начальном состоянии груз M находится ниже центра сферы на величину 
):
где R — радиус трубы, 
Отсюда
5. Груз m в точке отрыва еще движется по окружности радиусом R, но уже не давит на сферу. Поэтому его центростремительное ускорение вызвано только силой тяжести, так как сила направлена по касательной к сфере (см. рис.):
Подставляя сюда значение 
получим:
Отсюда 
Ответ: 30 г.
Спрятать критерииКритерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: закон сохранения механической энергии, формула для величины центростремительного ускорения); II) описаны все вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, и обозначений, используемых в условии задачи); III) представлен схематический рисунок с указанием сил, поясняющий решение; IV) проведены необходимые математические преобразования (допускается вербальное указание на их проведение) и расчеты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); V) представлен правильный ответ с указанием единиц измерения искомой величины | 3 |
| Правильно записаны необходимые положения теории и физические законы, закономерности; проведены необходимые преобразования, и представлен правильный ответ с указанием единиц измерения искомой величины. Но имеется один из следующих недостатков. Записи, соответствующие одному или нескольким пунктам: II, III, IV, — представлены не в полном объеме или отсутствуют. ИЛИ При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачеркнуты; не заключены в скобки, рамку и т. п.). ИЛИ При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца. ИЛИ При ПОЛНОМ решении отсутствует пункт V, или в нем допущена ошибка | 2 |
| Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи | 1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла | 0 |
| Максимальный балл | 3 |
Ответ: 30 г.
Раздел кодификатора ФИПИ/Решу ЕГЭ: 
Почему скорости грузов одинаковы,массы ведь разные..
Добрый день!
Это следствие кинематической связи. Грузики связаны нерастяжимой веревкой, а значит, расстояние, проходимое за небольшой интервал времени одним грузиком совпадает с расстоянием, проходимым другим. Это и ведет к равенству скоростей в любой момент времени.
А почему h - ho = π/6?
Ведь h - ho = R - Rcosα, разве нет?
Добрый день!
Только не
, а 
. Это соотношение результат того, что в силу нерастяжимости нити, груз 
опустится вниз ровно на такое же расстояние, какое проедет второй груз по сфере; 
— и есть это расстояние.
(2пиR x)/360
X это дуга в градусах
Градусная мера угла будет равна мере дуги. Если знаем дугу в градусах (например х) и радиус R, можем найти длину дуги, как долю длины окружности 2pi R * х/360
Поэтому (2пи R 30)/360=пиR/6
Добрый день! Ваше решение, безусловно, правильное. Но есть более простой способ решения.нарисовать три проекции. для первой N-mgcosx=ma(центростремительное) Отсюда при отрыве N=0. Для второй проекции T-Mg=-Ma и для третьей T-mgsinx=ma. и в принципе все. дальше математика. не нужно задумываться над изменением высоты и энергии.
Добрый день!
В Ваших втором и третьем уравнениях должно быть не то же ускорение, что в первом. В первом действительно стоит центростремительное. А вот в двух других — касательное. Которое определяет разгон. Так что все равно придется смотреть на энергию, чтобы выразить центростремительное ускорение. По сути, два Ваших дополнительных динамических уравнения оказываются лишними. Они привлекают в систему просто две новых неизвестных. Силу натяжения нити и касательное ускорение.
Добрый день!
Вы немного не поняли. во втором и третьем уравнении действительно ускорение не центростремительное а просто ускорение которое равно изменению скорости за время.(центростремительного на этих осях нету оно равно нулю для данной оси) то есть ускорение равно a= V^2 / S. Где S= ПR/6 . А V^2 =gRcosx (Это мы выражаем из центростремительного ускорения ось первая.) Таким образов все что имеем ( с учетом проекций ) подставляем друг в друга, так сказать совмещаем и получаем с учетом сокращений формулу m= M((6gcosx/ПИ) - g) / ((6gcosx/Пи)+gsinx) = 100*(16.56-10) / (16.56+10) = 656/21.5 =30 гр примерно)
Добрый день!
Не-не-не. Не обманывайте меня :)
Смотрите, что Вы делаете.
У вас есть два уравнения:
1)
для большого грузика
2)
для маленького грузика в проекции на ось, касательную к сфере.
Здесь
то самое ускорение, с которым сейчас двигается вниз большой груз (или что тоже самое, разгоняется по сфере маленький)
Сложим эти два уравнения:
Отсюда, в частности, видно, что ускорение
не является постоянным (зависит от угла, на который съехал маленький грузик), и каким-то очень сложным образом зависит от времени. А потому я вообще не понимаю, как вы его выразили через скорость в данный момент.
Более того, если переписать это уравнение в виде
и подставить Ваше
получается
Что не очень похоже на 30 г, которые Вы обещали :)
Добрый день!
Для начала давайте разберемся с начала)))
1)Ускорение по определению это изменение скорости деленное на время. а время в свою очередь это расстояние деленное на скорость. отсюда ускорение это v^2 / s.
Это ускорение действительно от времени зависит сложно. НО в момент отрыва уже не зависит от угла. а в момент отрыва v^2 = gRcosx. А s=пR/6. Отсюда и получаем выражение ускорения..)
2)Идем дальше. с проекциями
В момент отрыва который мы рассматриваем ускорение которое в знаменателе формулы отрицательное. т.е. m= M (g-a)/ (-a- gsinx) в вашем уравнении действительно все правильно кроме этого знака. и тогда в конечной формуле которая у вас написана будет в знаменателе -6(cosx)/П -sinx и в числителе кстати тоже при вычитание из 1 минус а минус дает плюс. отсюда m= 30 грамм)))
Добрый день!
Евгений, я очень надеюсь, что Вы сейчас меня разыгрываете, и реально так задачу решать не будете ))
По пунктам:
1) У Вас полная путаница со скоростями и ускорениями. Смотрите!
Если Вы поделите путь на время, Вы действительно получите скорость, но это будет средняя скорость. Она никоим образом не равна конечной скорости в произвольном случае. Как нам известно из кинематики, средняя скорость вообще плохо характеризует движение тела, именно по этой причине вводят понятие мгновенной скорости: как предел средней скорости на бесконечно малом интервале времени. Только если тело двигается равномерно, скорость (мгновенная) в любой момент времени совпадает со средней.
Аналогичная ситуация с ускорением. Если Вы поделите изменение скорости на время, вы получите ускорение, но это будет среднее ускорение. В случае равноускоренного движения среднее ускорение равно мгновенному, но у нас то не так, потому что ускорение во время движения меняется (с этим мы вроде разобрались).
Соответственное Ваши оба этапа получения формулы
неправильны.
2) Второй комментарий про знаки я не очень понял. Исходные уравнения записаны в проекции на такие оси, что ускорение проектируется "положительной величиной". А дальше, как Вы заметили, простая математика. Так что знаки вдогонку менять не нужно.
Здравствуйте. Я решал эту задачу без закона сохранения энергии, а просто расписал силы в момент отрыва (N=0) , определил длину дуги окружности, затем ускорение и получил в итоге ответ 50 г. А у вас 30 г. Причем вы сами решили эту задачу без З.С.Э. выше и получили 50 г. Как будет она оценена на ЕГЭ?
Как решается задача без з. с. э., если
и 
не постоянны?
50 г получается при подстановке неверного соотношения.
Добрый день.
Объясните пожалуйста, почему h-h0=R*(pi/6), а не R*cos(pi/6).
При съезжании вниз по сфере груз
проделывает путь 
, груз 
опускается вниз на 
, поскольку нить нерастяжима.