Тип Д29 C2 № 9165 
Механика (расчетная задача). Динамика
i
Какое ускорение a поступательного движения можно сообщить однородному кубику, находящемуся на шероховатой горизонтальной плоскости, прикладывая к его верхнему ребру горизонтальную силу в плоскости симметрии кубика (см. рис.)? Коэффициент трения кубика о плоскость равен 
= 0,4.
Решение.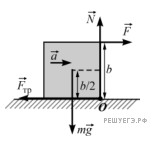 
1. При движении однородного кубика массой m по шероховатой горизонтальной плоскости на него действуют, кроме горизонтальной силы 
вертикальные сила тяжести 
приложенная в центре кубика, сила 
нормального давления со стороны плоскости, а также горизонтальная сила сухого трения скольжения, равная по модулю, согласно закону Амонтона — Кулона, 
2. Для того чтобы кубик двигался поступательно, не опрокидываясь, сила 
и создаваемое ею ускорение 
не должны превышать некоторого предела, зависящего от коэффициента трения кубика о плоскость. В предельном случае, перед опрокидыванием, силы и 
будут приложены к переднему нижнему ребру О кубика (см. рис.), и опрокидывающий момент сил и будет компенсироваться возвращающим моментом силы относительно оси, проходящей через центр масс кубика: 
Здесь b — длина ребра кубика, 
3. Уравнение движения кубика, то есть второй закон Ньютона в проекциях на горизонтальное и вертикальное направления, при этом имеет вид: 
и 
4. Из написанных уравнений получаем:
Ответ: 
Примечание.
Если выбрать другую ось, относительно которой рассчитывать моменты сил, то по теореме Вариньона суммарный момент сил не равен нулю, поскольку кубик движется с ускорением. Суммарный момент равен моменту равнодействующей силы. Например, для оси, проходящей через точку O:
С учетом того, что 
и 
получаем
Спрятать критерииКритерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона и кинематические соотношения); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчеты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины | 3 |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объеме или отсутствуют. И ( ИЛИ ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачеркнуты; не заключены в скобки, рамку и т. п.). И ( ИЛИ ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И ( ИЛИ ) Отсутствует пункт IV, или в нем допущена ошибка | 2 |
| Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи | 1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла | 0 |
| Максимальный балл | 3 |
Ответ: 
